UPDATE!
Triangle Formulas : Right Triangle
C = A + B = Pi/2 radians = 90 degrees
c^2 = a^2 + b^2
P = a + b + c
s = (a+b+c)/2
K = ab/2
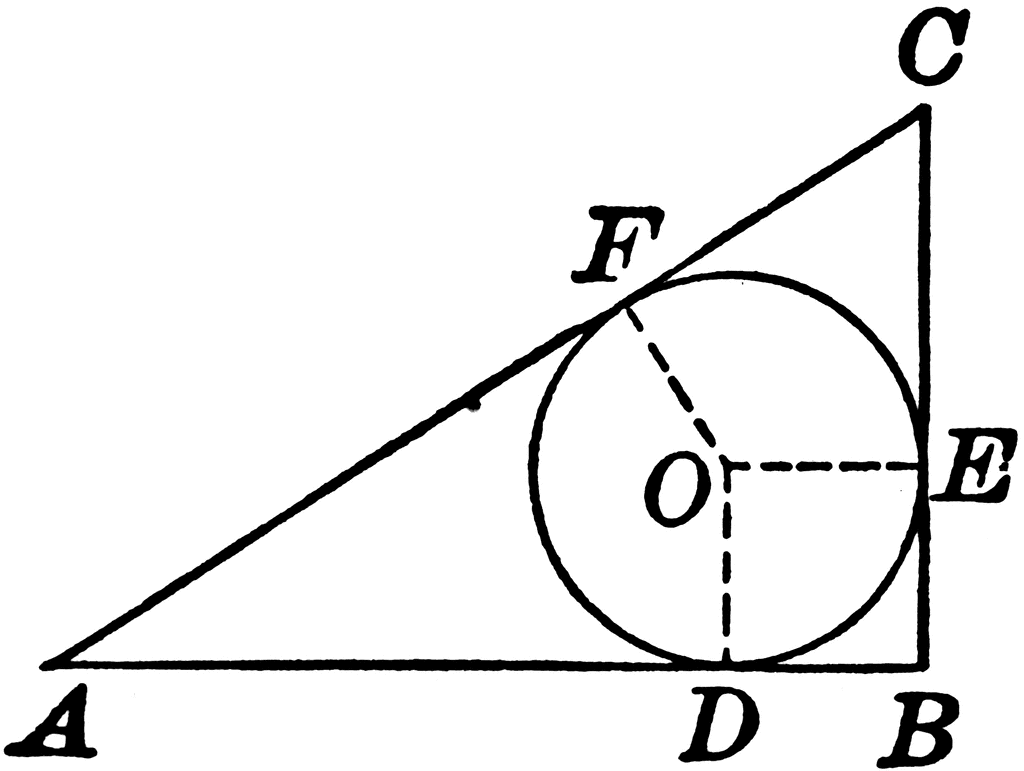
Circle Inscribed in a Right Triangle
We can write,
r = ab/(a + b + c) with c = sqrt(a^2 + b^2)
d = sqrt((a - 2r)^2+(b - 2r)^2)
OR
r = (a + b - c)/2 where c = Sqrt(a^2 + b^2)
Then (a - 2r)^2 + (b - 2r)^2 = (c - a)^2 + (c - b)^2 etc
Two ways to solve this one, first, find the radius of the inscribed circle using
ReplyDeleteSqrt[((s - a) (s - b) (s - c))/s] where s=semi perimeter and sides 5,12,13 gives a radius of 2. So centre of first circle would be 2,2, and we can work out the centre of the second to be 10,3. The distance between centres would then be.
Sqrt(65).
We could also use the cartesian co-ordinates equation of the co-ordinates of the incircle
xi,yi =
a*x1+b*x2+c*x3/a+b+c, a*y1+b*y2+c*y3/a+b+c
substituting the appropriate sides and co-ordiantes will give us centres at 2,2 and 10,3.
We would get 60/30,60/30 and 300/30, 90/30 using the co-ordinates 0,0, 12,0, 12,5 and 0,5.
Paul