2 semicircles, 1 isosceles triangle

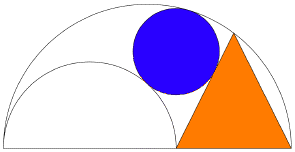
Consider two semicircles S and T that emanate from the same point with diameters along a common line, with S being the larger.

Draw an isosceles triangle whose base is the part of diameter of S that is outside T and whose apex is on S. Draw a circle inside S that is tangent to S, T, and the triangle.

Prove that the center of this circle is directly above the point common to the triangle and T