Monday, February 28, 2011
Geometry
(1) Equilateral Triangles
Van Schooten's and Pompeiu's Theorems
An Extension of van Schooten's Theorem
Ptolemy's Theorem
Fermat point
The Fermat Point and Generalizations
Julia Maps
Google Labs: Explore Julia set like a Google Map
http://juliamap.googlelabs.com/#ll=-5.178482,-8.964844$z=2$p=ffffff,ffffff,ffffff,ffffff,ff0000,ffff00,ffff00,ff00,ff$f=mandelbrot
http://juliamap.googlelabs.com/#ll=-5.178482,-8.964844$z=2$p=ffffff,ffffff,ffffff,ffffff,ff0000,ffff00,ffff00,ff00,ff$f=mandelbrot
A prime number p can be expressed as a sum...
Every prime of the form 4n+1 is a sum of two squares.
There's also the "four squares theorem", ie, every prime is a sum of four squares
This is known as the "two squares theorem"
What are these math expressions
(1)
What's
0 + 1 - (2 * 3 / 4) + 5 - (6 * 7 / 8) + 9 - (10 * 11 / 12) + ... - (18 * 19 / 20)?
Is there a pattern if you continue it out?
(2)
What is
cos(Pi/3) * cos(Pi/4) * cos(Pi/5) * cos(Pi/6)* cos(Pi/7) *....?
Math in pictures
(1)
Sine on the side of a building in Pittsburgh, PA.
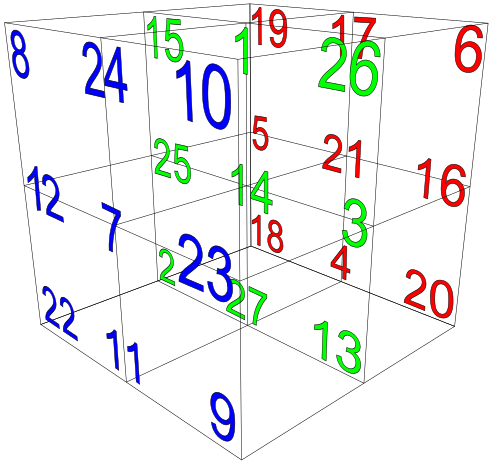
(2) 42
The 3 × 3 × 3 magic cube with rows summing to 42.

(3) Fibonacci
Sine on the side of a building in Pittsburgh, PA.
(4) Dunbar's number
Test Yourself | Math
Test your math skills with today’s question, created by Bobson Wong at Math for America from the article “Fleas’ ‘Feet’ Unleash That Spectacular Leap.”
Math News - University of Waterloo, Canada
http://www.mathnews.uwaterloo.ca/
N things to make a romance more awesome
Jeopardy Game to Decide Fate of Humanity
Good Idea, Awful Idea
Discoveries & Breakthroughs inside Math
How does math play a role in the formation of snowflakes, in why 9 out of 10 dentists agree, or in how you design your new patio? Discoveries & Breakthrough Inside Math is the result of a partnership between the Mathematical Association of America, the American Statistical Association, the Society for Industrial and Applied Mathematics, and the American Institute of Physics' Discoveries and Breakthroughs Inside Science (DBIS) program. This site features video segments based on the latest mathematical research and applications that are currently being distributed to local TV stations across the USA and around the world.
Odds Of Winning
Latest stories :
Secrets of Snowflakes
Saving Time, Tax Payers' Money, & Jobs
Time Change: Setting Your Internal Clock
Forecasting Floods in 3D
Sunday, February 27, 2011
Saturday, February 26, 2011
Hexagonal Number
http://mathworld.wolfram.com/HexagonalNumber.html
Show that every positive integer can be expressed as a sum of 6 hexagonal numbers.
Pentagonal Number
A polygonal number of the form n*(3n - 1)/2
0, 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151
Questions:
(*) Find how pentagonal numbers relate to triangular numbers
(*) Show that every positive integer can be expressed as a sum of 5 or fewer pentagonal numbers
0, 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151
There are conjectured to be exactly 210 positive integers that cannot be represented using three pentagonal numbers, namely
There are six positive integers that cannot be expressed using four pentagonal numbers
Questions:
(*) Find how pentagonal numbers relate to triangular numbers
(*) Show that every positive integer can be expressed as a sum of 5 or fewer pentagonal numbers
Triangular Numbers
http://www.shyamsundergupta.com/triangle.htm
Find any interesting equations that relate T(a+b) To T(a) and T(b), and T(a*b)
Pollock's Conjecture
Pollock’s Conjecture (1850) states that every number is the sum of at most 5 tetrahedral numbers; this conjecture has not yet been proven. It is also conjectured that there are exactly 241 numbers that cannot be written as the sum of 4 or fewer tetrahedral numbers.
The conjecture is almost certainly true, but has not yet been proven.
The conjecture is almost certainly true, but has not yet been proven.
Tetrahedral number
http://en.wikipedia.org/wiki/Tetrahedral_number
0, 1, 4, 10, 20, 35, 56, 84, 120, 165, 220, 286, 364, 455, 560, 680, 816, 969, 1140, 1330, 1540, 1771, 2024, 2300, 2600, 2925, 3276, 3654, 4060, 4495, 4960, 5456, 5984, 6545, 7140, 7770, 8436, 9139, 9880, 10660, 11480, 12341, 13244, 14190, 15180
A.J. Meyl proved in 1878 that only three tetrahedral numbers are also perfect squares, namely:
T1 = 1^2 = 1
T2 = 2^2 = 4
T48 = 140^2 = 19600.
The only tetrahedral number that is also a square pyramidal number is 1 (Beukers, 1988), and the only tetrahedral number that is also a perfect cube is 1.
A.J. Meyl proved in 1878 that only three tetrahedral numbers are also perfect squares, namely:
T1 = 1^2 = 1
T2 = 2^2 = 4
T48 = 140^2 = 19600.
The only tetrahedral number that is also a square pyramidal number is 1 (Beukers, 1988), and the only tetrahedral number that is also a perfect cube is 1.
Squares formed by concatenation of consecutive number
concatenation of 2 consecutive numbers, 183 and 184
428^2 = 183,184
428^2 = 183,184
Extravagant / Economical numbers
An extravagant number is one for which the prime factorization (including powers) requires more digits that the original number such as 30 = 2*3*5 (compare to economical number).
http://primes.utm.edu/glossary/page.php?sort=ExtravagantNumber
http://primes.utm.edu/glossary/page.php?sort=ExtravagantNumber
Math Quotes #2
Puzzle: 8 digits
Place the number cards in the rectangles below so that no two consecutive numbers are next to each other horizontally, vertically, or diagonally. For example, if the 5 is placed in the far left box, then the 4 or 6 can't be placed in the box directly to the right of the 5 or the two boxes that are diagonally above and below the 5.


Friday, February 25, 2011
Open problem about Pythagorean triangles
Definitions :
Square number
http://en.wikipedia.org/wiki/Square_number
It asks for Pythagorean triangles with a triangular number and a square for legs, and a pentagonal number n(3n - 1)/2 for hypothenuse.
Square number
http://en.wikipedia.org/wiki/Square_number
Pythagorean Triangles and Triples
http://oeis.org/A000326
0, 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151
Triangular number
Pentagonal number
Triangular numbers:
http://oeis.org/A000217
http://oeis.org/A000217
0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153, 171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, 435, 465, 496, 528, 561, 595, 630, 666, 703, 741, 780, 820, 861, 903, 946, 990, 1035, 1081, 1128, 1176, 1225, 1275, 1326, 1378, 1431
Pentagonal numbers: n(3n-1)/2 :http://oeis.org/A000326
0, 1, 5, 12, 22, 35, 51, 70, 92, 117, 145, 176, 210, 247, 287, 330, 376, 425, 477, 532, 590, 651, 715, 782, 852, 925, 1001, 1080, 1162, 1247, 1335, 1426, 1520, 1617, 1717, 1820, 1926, 2035, 2147, 2262, 2380, 2501, 2625, 2752, 2882, 3015, 3151
The Open problem:
Are there any nontrivial examples besides (3,4,5) and (105,100,145)?
Does it help to allow pentagonal numbers of negative rank, n(3n + 1)/2?
Does it help to allow pentagonal numbers of negative rank, n(3n + 1)/2?
Unsolved problem about Polygonal Numbers
Every Number is Expressible as the Sum of How Many Polygonal Numbers?
Thursday, February 24, 2011
Pronic number
A pronic number is a number which is the product of two consecutive integers,
is a product of two consecutive integers.
that is, n*(n + 1).
For every integer a, prove that
(a^2 + a - 1)(a^2 + 3a + 1) + 1
is a product of two consecutive integers.
Square of 2 consecutive numbers using the same digits
Here are squares of 2 consecutive numbers that use the same digits:
Others:
Could you find others?
157^2 = 24,649 .... 158^2 = 24,964.
Others:
13^2 = 169 ... 14^2 = 196
913^2 = 833,569 ... 914^2 = 835,396
Could you find others?
Superparticular number
(n + 1)/n = 1 + 1/n
These ratios are also important in visual harmony. Most flags of the world's countries have a ratio of 3:2 between their length and height
Here are examples of flags with ratios other than 3:2
Ratio 1:1 Vatican City
Here are examples of flags with ratios other than 3:2
Ratio 1:1 Vatican City
Check the other ratios at
Of squares and consecutive cubes
(1)
Let n be any natural number whose square is also the difference between two consecutive cubes.
Prove that 2n-1 is also a square.
(2)
Show that the cube of every positive integer n is the difference of two consecutive cubes minus a cube
Sum of digits of a 2-digit number
The sum of the digits of a 2-digit integer N is S and the product of the digits is P.
One of the differences N - S and N - P is a square and the other is a cube.
One of the differences N - S and N - P is a square and the other is a cube.
Find N and show it to be unique.
4-digit integers: Squares of their digits
Take a random 4-digit integer (abcd),
then calculate a^2 + b^2 + c^2 + d^2
For example, 7283
then 7^2 + 2^2 + 8^2 + 3^2 = 126
Repeat the process
1^2 + 2^2 + 6^2 = 41
4^2 + 1^2 = 17
1^2 + 7^2 = 50
5^2 + 0^2 = 25
2^2 + 5^2 = 29
2^2 + 9^2 = 85
8^2 + 5^2 = 89
8^2 + 9^2 = 145
The sequence is 126, 41, 17, 50, 25, 29, 85, 89, 145
145 --> 1^2 + 4^2 + 5^2 = 42
42 ---> 4^2 + 2^2 = 20
20 ---> 2^2 + 0^2 = 4
4 ----> 4^2 = 16
16 ---> 1^2 + 6^2 = 37
37 ---> 3^2 + 7^2 = 58
58 ---> 5^2 + 8^2 = 89
89 ---> 8^2 + 9^2 = 145
It will either end in 1 or with 145
then calculate a^2 + b^2 + c^2 + d^2
For example, 7283
then 7^2 + 2^2 + 8^2 + 3^2 = 126
Repeat the process
1^2 + 2^2 + 6^2 = 41
4^2 + 1^2 = 17
1^2 + 7^2 = 50
5^2 + 0^2 = 25
2^2 + 5^2 = 29
2^2 + 9^2 = 85
8^2 + 5^2 = 89
8^2 + 9^2 = 145
The sequence is 126, 41, 17, 50, 25, 29, 85, 89, 145
145 --> 1^2 + 4^2 + 5^2 = 42
42 ---> 4^2 + 2^2 = 20
20 ---> 2^2 + 0^2 = 4
4 ----> 4^2 = 16
16 ---> 1^2 + 6^2 = 37
37 ---> 3^2 + 7^2 = 58
58 ---> 5^2 + 8^2 = 89
89 ---> 8^2 + 9^2 = 145
It will either end in 1 or with 145
Cubes using the same digits
For example,
102^3 = 1,061,208 .......... 201^3 = 8,120,601.
178^3 = 5,639,752 .......... 196^3 = 7,529,536
Investigate to find other examples.
Digits of 3-digit integers
Notice that
147 = 14^2 – 7^2 = (14 + 7) * 7, where 14 = 7 * 2
147 * (14 + 7) = 14^3 + 7^3 = 3087.
148 * (14 + 8) = 14^3 + 8^3 = 3256
Investigate to find other examples.
147 = 14^2 – 7^2 = (14 + 7) * 7, where 14 = 7 * 2
147 * (14 + 7) = 14^3 + 7^3 = 3087.
148 * (14 + 8) = 14^3 + 8^3 = 3256
Investigate to find other examples.
Using the digits from 1 to 9 only once
879 + 426 = 1305 and 879 + 624 = 1503
859 + 347 = 1206 and 859 + 743 = 1602
789 + 264 = 1053 and 789 + 246 = 1035
756 + 342 = 1098 and 765 + 324 = 1089
657 + 432 = 1089 and 675 + 423 = 1098
589 + 473 = 1062 and 589 + 437 = 1026
Find other combinations.
With products,
58401 = 63 * 927 32890 = 46 * 715 26910 = 78 * 345
19084 = 52 * 367 17820 = 36 * 495 and 17820 = 45 * 396
16038 = 27 * 594 and 16038 = 54 * 297 15678 = 39 * 402
65821 = 7 * 9403 65128 = 7 * 9304 34902 = 6 * 5817
36508 = 4 * 9127 28651 = 7 * 4093 28156 = 4 * 7039
27504 = 3 * 9168 24507 = 3 * 8169 21658 = 7 * 3094
20754 = 3 * 6918 20457 = 3 * 6819 17082 = 3 * 5694
15628 = 4 * 3907
859 + 347 = 1206 and 859 + 743 = 1602
789 + 264 = 1053 and 789 + 246 = 1035
756 + 342 = 1098 and 765 + 324 = 1089
657 + 432 = 1089 and 675 + 423 = 1098
589 + 473 = 1062 and 589 + 437 = 1026
Find other combinations.
With products,
58401 = 63 * 927 32890 = 46 * 715 26910 = 78 * 345
19084 = 52 * 367 17820 = 36 * 495 and 17820 = 45 * 396
16038 = 27 * 594 and 16038 = 54 * 297 15678 = 39 * 402
65821 = 7 * 9403 65128 = 7 * 9304 34902 = 6 * 5817
36508 = 4 * 9127 28651 = 7 * 4093 28156 = 4 * 7039
27504 = 3 * 9168 24507 = 3 * 8169 21658 = 7 * 3094
20754 = 3 * 6918 20457 = 3 * 6819 17082 = 3 * 5694
15628 = 4 * 3907
Square numbers using the same digits #2
Older post
http://benvitale-funwithnum3ers.blogspot.com/2011/01/square-numbers-using-same-digits.html245^2 = 60025 ..... 160^2 = 25600 ..... 250^2 = 62500
Update:
148^2 = 21904 .... 203^2 = 41209 .... 302^2 = 91204.
130^2 = 16900 ... 140^2 = 19600 ... 310^2 = 96100,
103^2 = 10609 ... 247^2 = 61009 ... 301^2 = 90601.
12^2 = 144 ..... 21^2 = 441
102^2 = 10404 ... 120^2 = 14400 ... 201^2 = 40401 ... 210^2 = 44100.
108^2 = 11664 .... 129^2 = 16641 .... 204^2 = 41616.
154^2 = 23716 .... 181^2 = 32761 .... 2692^ = 72361
135^2 = 18225 ..... 159^2 = 25281 ..... 285^2 = 81225
13^2 = 169 ..... 14^2 = 196 ..... 31^2 = 961
128^2 = 16,384 ... 178^2 = 31,684 ... 191^2 = 36,481 ... 196^2 = 38,416,
209^2 = 43,681.
Manipulating digits from 1 to 9 to find prime numbers
Use the basic arithmetic operations and include the more advanced operations to find prime numbers
For example,
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 = 3^2 * 5
9! + 8! + 7! + 6! + 5! + 4! + 3! + 2! + 1! = 409113 = 3^2 * 131 * 347
9! + 8! + 7! + 6! + 5! + 4! + 3! + 2! - 1! = 409111 = 569 * 719
9! + 8! + 7! + 6! + 5! + 4! + 3! - 2! + 1! = 409109 = 37 * 11057
9! + 8! + 7! + 6! + 5! + 4! + 3! - 2! - 1! = 409107 = 3 * 31 * 53 * 83
9! + 8! + 7! + 6! + 5! + 4! - 3! + 2! + 1! = 409101 = 3 * 7 * 7 * 11 * 11 * 23
9! + 8! + 7! + 6! + 5! + 4! - 3! - 2! + 1! = 409097 = 13 * 31469
9! + 8! + 7! + 6! + 5! + 4! - 3! - 2! - 1! = 409095 = 3 * 3 * 5 * 9091
9^8 + 7^6 + 5^4 + 3^2 + 1 = 43165005 = 3 * 5 * 13 * 41 * 5399
(No prime number so far)
9 - 8 + 7 - 6 + 5 - 4 + 3 - 2 + 1 = 5 is a prime number.
9 + 8^7 + 6^5 + 4^3 + 2^1 = 2105003 is a prime number
10! - 9! + 8! - 7! + 6! - 5! + 4! - 3! + 2! - 1! = 3301819 is a prime number
9! + 8! + 7! + 6! + 5! + 4! - 3! + 2! - 1! = 409099 is a prime number
Investigate with other combinations
For example,
9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45 = 3^2 * 5
9! + 8! + 7! + 6! + 5! + 4! + 3! + 2! + 1! = 409113 = 3^2 * 131 * 347
9! + 8! + 7! + 6! + 5! + 4! + 3! + 2! - 1! = 409111 = 569 * 719
9! + 8! + 7! + 6! + 5! + 4! + 3! - 2! + 1! = 409109 = 37 * 11057
9! + 8! + 7! + 6! + 5! + 4! + 3! - 2! - 1! = 409107 = 3 * 31 * 53 * 83
9! + 8! + 7! + 6! + 5! + 4! - 3! + 2! + 1! = 409101 = 3 * 7 * 7 * 11 * 11 * 23
9! + 8! + 7! + 6! + 5! + 4! - 3! - 2! + 1! = 409097 = 13 * 31469
9! + 8! + 7! + 6! + 5! + 4! - 3! - 2! - 1! = 409095 = 3 * 3 * 5 * 9091
9^8 + 7^6 + 5^4 + 3^2 + 1 = 43165005 = 3 * 5 * 13 * 41 * 5399
(No prime number so far)
9 - 8 + 7 - 6 + 5 - 4 + 3 - 2 + 1 = 5 is a prime number.
9 + 8^7 + 6^5 + 4^3 + 2^1 = 2105003 is a prime number
10! - 9! + 8! - 7! + 6! - 5! + 4! - 3! + 2! - 1! = 3301819 is a prime number
9! + 8! + 7! + 6! + 5! + 4! - 3! + 2! - 1! = 409099 is a prime number
Investigate with other combinations
Filzian number
A Filzian number is a positive integer that is equal to sum
of its digits times the product of its digits.
For example,
(1 + 3 + 5) * 1 * 3 * 5 = 135
(1 + 4 + 4) * 1 * 4 * 4 = 144
(a) Find another one
(b) Find a general solution
of its digits times the product of its digits.
For example,
(1 + 3 + 5) * 1 * 3 * 5 = 135
(1 + 4 + 4) * 1 * 4 * 4 = 144
(a) Find another one
(b) Find a general solution
Reversible numbers and their squares
For example,
12^2 = 144 and 21^2 = 441.
Also: 102^2 = 10404, 120^2 = 14400,
201^2 = 40401 and 210^2 = 44100
Investigate to find other examples.
12^2 = 144 and 21^2 = 441.
Also: 102^2 = 10404, 120^2 = 14400,
201^2 = 40401 and 210^2 = 44100
Investigate to find other examples.
Sudoku
>> What is the minimal number of digits guaranteeing a unique solution?
The mallest known number of clues a sudoku puzzle can have and still be solvable is 17. Gordon Royle maintains a database of all known puzzles, 48862 so far, but has yet to find a 16 clue puzzle.
Sudoku Fridays
The mallest known number of clues a sudoku puzzle can have and still be solvable is 17. Gordon Royle maintains a database of all known puzzles, 48862 so far, but has yet to find a 16 clue puzzle.
Minimum Sudoku
Wednesday, February 23, 2011
Catalan Numbers
 Source: http://milan.milanovic.org/math/english/fibo/fibo4.html
Source: http://milan.milanovic.org/math/english/fibo/fibo4.htmlIn how many ways can a collection of parentheses appear in a sentence?
(1)
In how many ways can you cut up a regular hexagon (6-sided polygon) into triangles using 3 nonintersecting diagonals?
For example, there are 5 ways for a pentagon
(2)
Let's say 20 people show up to go see the $5 matinee at the local theater.
Suppose that 10 of these people have exact change, but the other 10 have only a $10 bill,and will require change. Unfortunately, on this particular day the cashier has forgotten to stop at the bank and so he has no change to start with. What are the odds that he will be able to sell all 20 people tickets without running out of change?
Kaprekar numbers
In mathematics, a Kaprekar number for a given base is a non-negative integer, the representation of whose square in that base can be split into two parts that add up to the original number again.
For example,
1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777, 9999, 17344, 22222, 38962, 77778, 82656, 95121, 99999, 142857, 148149, 181819, 187110, 208495, 318682, 329967, 351352, 356643, 390313, 461539, 466830, 499500, 500500, 533170
... are the Kaprekar numbers
Because
9^2 = 81 and 8 + 1 = 9
45^2 = 2025 and 20 + 25 = 45
55^2 = 3025 and 30 + 25 = 55
99^2 = 9801 and 98 + 01 = 99
........................................
........................................
703^2 = 494209 and 494 + 209 = 703
The Indian mathematician D.R.Kaprekar made the following discovery in 1949.
(1) Take a four-digit number with different digits (acbd with a < b < c < d)
You'll get 6174 in no more than 7 steps.
Investigate in other bases.
For example,
1, 9, 45, 55, 99, 297, 703, 999, 2223, 2728, 4879, 4950, 5050, 5292, 7272, 7777, 9999, 17344, 22222, 38962, 77778, 82656, 95121, 99999, 142857, 148149, 181819, 187110, 208495, 318682, 329967, 351352, 356643, 390313, 461539, 466830, 499500, 500500, 533170
... are the Kaprekar numbers
Because
9^2 = 81 and 8 + 1 = 9
45^2 = 2025 and 20 + 25 = 45
55^2 = 3025 and 30 + 25 = 55
99^2 = 9801 and 98 + 01 = 99
........................................
........................................
703^2 = 494209 and 494 + 209 = 703
Theorem 1:
k is in K(N) if and only if k = d Inv(d, (N-1)/d) for some unitary divisor d of N - 1
Theorem 2:
Every even perfect number is a Kaprekar number in the binary base.
(2)
The Indian mathematician D.R.Kaprekar made the following discovery in 1949.
(1) Take a four-digit number with different digits (acbd with a < b < c < d)
You'll get 6174 in no more than 7 steps.
Investigate in other bases.
Consecutive numbers
8281 = 91^2
183184 = 428^2
328329 = 573^2
528529 = 727^2
715716 = 846^2
60996100 = 7810^2
82428241 = 9079^2
98029801 = 9901^2
1322413225 = 36365^2
4049540496 = 63636^2
183184 = 428^2
328329 = 573^2
528529 = 727^2
715716 = 846^2
60996100 = 7810^2
82428241 = 9079^2
98029801 = 9901^2
1322413225 = 36365^2
4049540496 = 63636^2
Mirror numbers
Notice the following examples:
12^2 = 144 ........................ 21^2 = 441
13^2 = 169 ........................ 31^2 = 961
102^2 = 10404 ................. 201^2 = 40401
103^2 = 10609 ................. 301^2 = 90601
112^2 = 12544 ................. 211^2 = 44521
113^2 = 12769 ................. 311^2 = 96721
1012^2 = 1024144 ........... 2101^2 = 4414201
1112^2 = 1236544 ........... 2111^2 = 4456321
1212^2 = 1468944 ........... 2121^2 = 4498641
2012^2 = 4048144 ........... 2102^2 = 4418404
21^2 - 12^2 = 441 - 144 = 297
31^2 - 13^2 = 961 - 169 = 792
If x and y are mirror numbers and their product x * y = 53703
then x= 153 and y = 531
How do you go about it to find these two numbers?
Notice that
The factors of 53703 are:
1 3 9 13 17 27 39 51 81 117 153 221 243 351 459 663 1053 1377 1989 3159 4131
5967 17901 53703
The prime factors are: 3 * 3 * 3 * 3 * 3 * 13 * 17
(1)
13^2 = 169 ........................ 31^2 = 961
102^2 = 10404 ................. 201^2 = 40401
103^2 = 10609 ................. 301^2 = 90601
112^2 = 12544 ................. 211^2 = 44521
113^2 = 12769 ................. 311^2 = 96721
1012^2 = 1024144 ........... 2101^2 = 4414201
1112^2 = 1236544 ........... 2111^2 = 4456321
1212^2 = 1468944 ........... 2121^2 = 4498641
2012^2 = 4048144 ........... 2102^2 = 4418404
(2)
21^2 - 12^2 = 441 - 144 = 297
31^2 - 13^2 = 961 - 169 = 792
Could find other examples?
(3)
If x and y are mirror numbers and their product x * y = 53703
then x= 153 and y = 531
How do you go about it to find these two numbers?
Notice that
The factors of 53703 are:
1 3 9 13 17 27 39 51 81 117 153 221 243 351 459 663 1053 1377 1989 3159 4131
5967 17901 53703
The prime factors are: 3 * 3 * 3 * 3 * 3 * 13 * 17
Polite number
In number theory, a polite number is a positive integer that can be written as the sum of two or more consecutive positive integers. Other positive integers are impolite...
For example,
6 = 1 + 2 + 3, 18 = 3 + 4 + 5 + 6, 41= 20 + 21 are all polite.
On the other hand 8 is not polite so is called an impolite number.
Is every odd number greater than one polite? Why?
For example,
6 = 1 + 2 + 3, 18 = 3 + 4 + 5 + 6, 41= 20 + 21 are all polite.
On the other hand 8 is not polite so is called an impolite number.
Is every odd number greater than one polite? Why?
Paul Cohen : Continuum Hypothesis
Paul Cohen talks about working on the Continuum Hypothesis and his interaction with Kurt Gödel. From the Gödel Centennial, Vienna, 2006.
Paul Joseph Cohen biography
Paul Joseph Cohen biography
*Cantor Hypothesis: any infinite subset of the set of R can be put into 1-to-1 correspondence either with the set of integers or with the set of all real numbers.
Cohen proved the Continuum Hypothesis and the Axiom of Choice actually are undecidable using the axioms of set theory
Cohen proved the Continuum Hypothesis and the Axiom of Choice actually are undecidable using the axioms of set theory
Part 1 of 6
Part 2 of 6
Part 3 of 6
Part 4 of 6
Part 5 of 6
Part 6 of 6
Tuesday, February 22, 2011
Unit Square, Unit Cube
(1) What region inside a unit square has the greatest ratio of area to perimeter?
(2) What volume inside a unit cube has the greatest ratio of volume to surface area?
(2) What volume inside a unit cube has the greatest ratio of volume to surface area?
Tennis Math
Two evenly matched tennis players are playing a tiebreak set.
The server in any game wins each point with a fixed probability p,
where 0 < p < 1
Related topic :
Teaching Mathematics and Statistics Using Tennis
The server in any game wins each point with a fixed probability p,
where 0 < p < 1
For what values of p and score situations during a set can the player ahead according to the score have less than a 50% chance of winning the set?
Related topic :
Find a 3-digit number...
... that has the following property:
Divide the number by 3,
reverse the digits of the result,
subtract 1 and you produce the original number.
What is the number and what is the next greater number (possibly with more than three digits) having this property?
Divide the number by 3,
reverse the digits of the result,
subtract 1 and you produce the original number.
What is the number and what is the next greater number (possibly with more than three digits) having this property?
Unusual Magic Squares
http://www.magic-squares.net/unususqr.htm
Here's a puzzle:
Place the numbers from 1 to 15 in the 3 X 5 array so that each column has
Here's a puzzle:
Place the numbers from 1 to 15 in the 3 X 5 array so that each column has
the same sum and each row has the sum
_ _ _ _ _
_ _ _ _ _
_ _ _ _ _
Martin Gardner: Words to Numbers
Take any whole number and write out its numeral in
English, such as FIVE for the usual 5.
Count the number of characters in the spelling.
In this case, it is 4 — or FOUR.
So, work now with the 4 or FOUR.
Repeat with 4 to get 4 again.
Take, ONE HUNDRED SIXTY-THREE for a total count of 23.
(Include spaces and hyphens in your count.)
ONE HUNDRED SIXTY-THREE -> TWENTY THREE -> TWELVE -> SIX -> THREE -> FIVE -> FOUR.
Try with any other number, and see if it always works
In English we end up with 4 as the final number. It would be interesting to find out what numbers we end up in other languages.
Since I'm fluent in Italian and in French, I'll find out.
Try it in Italian:
Italian Cardinal Numbers: 1 - 100
1 ............... uno ............... (=3)
2 ............... due ............. (=3)
3 ............... tre ............. (=3)
4 ............... quattro ......... (=7)
5 ............... cinque .......... (=6)
6 ............... sei ............. (=3)
7 ............... sette ........... (=5)
8 ............... otto ............ (=4)
9 ............... nove ............ (=4)
10 ............... dieci .......... (=5)
11 ............... undici ......... (=6)
12 ............... dodici ......... (=6)
13 ............... tredici ........ (=7)
14 ............... quattordici ..... (=11)
15 ............... quindici ........ (=8)
16 ............... sedici .......... (=6)
17 ............... diciassette
18 ............... diciotto
19 ............... diciannove
20 ............... venti
21 ............... ventuno
22 ............... ventidue
23 ............... ventitré
24 ............... ventiquattro
25 ............... venticinque
26 ............... ventisei
27 ............... ventisette
28 ............... ventotto
29 ............... ventinove
30 ............... trenta
40 ............... quaranta
50 ............... cinquanta
60 ............... sessanta
70 ............... settanta
80 ............... ottanta
90 ............... novanta
100 ............... cento
The numbers venti, trenta, quaranta, cinquanta, and so on drop the final vowel when combined with uno and otto. Tre is written without an accent, but ventitré, trentatré, and so on are written with an accent.
So, if we start with 5 or CINQUE (=6) ->
Numbers 1 - 100 in French
1 ... un ............................. 11 ... onze
2 ... deux ........................... 12 ... douze
3 ... trois .......................... 13 ... treize
4 ... quatre ......................... 14 ... quatorze
5 ... cinq ........................... 15 ... quinze
6 ... six ............................ 16 ... seize
7 ... sept ........................... 17 ... dix-sept
8 ... huit ........................... 18 ... dix-huit
9 ... neuf ........................... 19 ... dix-neuf
10 ... dix ........................... 20 ... vingt
21 ... vingt et un ........................ 31 ... trente et un
22 ... vingt-deux ......................... 32 ... trente-deux
23 ... vingt-trois ........................ 33 ... trente-trois
24 ... vingt-quatre ....................... 34 ... trente-quatre
25 ... vingt-cinq ......................... 35 ... trente-cinq
26 ... vingt-six .......................... 36 ... trente-six
27 ... vingt-sept ......................... 37 ... trente-sept
28 ... vingt-huit ......................... 38 ... trente-huit
29 ... vingt-neuf ......................... 39 ... trente-neuf
30 ... trente ............................. 40 ... quarante
41 ... quarante et un ........................... 51 ... cinquante et un
42 ... quarante-deux ............................ 52 ... cinquante-deux
43 ... quarante-trois ........................... 53 ... cinquante-trois
44 ... quarante-quatre .......................... 54 ... cinquante-quatre
45 ... quarante-cinq ............................ 55 ... cinquante-cinq
46 ... quarante-six ............................. 56 ... cinquante-six
47 ... quarante-sept ............................ 57 ... cinquante-sept
48 ... quarante-huit ............................ 58 ... cinquante-huit
49 ... quarante-neuf ............................ 59 ... cinquante-neuf
50 ... cinquante ................................ 60 ... soixante
61 ... soixante et un ........................... 71 ... soixante et onze
62 ... soixante-deux ............................ 72 ... soixante-douze
63 ... soixante-trois ........................... 73 ... soixante-treize
64 ... soixante-quatre .......................... 74 ... soixante-quatorze
65 ... soixante-cinq ............................ 75 ... soixante-quinze
66 ... soixante-six ............................. 76 ... soixante-seize
67 ... soixante-sept ............................ 77 ... soixante-dix-sept
68 ... soixante-huit ............................ 78 ... soixante-dix-huit
69 ... soixante-neuf ............................ 79 ... soixante-dix-neuf
70 ... soixante-dix ............................. 80 ... quatre-vingts
80 ... quatre-vingts ......................... 91 ... quatre-vingt-onze
81 ... quatre-vingt-un ....................... 92 ... quatre-vingt-douze
82 ... quatre-vingt-deux ..................... 93 ... quatre-vingt-treize
83 ... quatre-vingt-trois .................... 94 ... quatre-vingt-quatorze
84 ... quatre-vingt-quatre ................... 95 ... quatre-vingt-quinze
85 ... quatre-vingt-cinq ..................... 96 ... quatre-vingt-seize
86 ... quatre-vingt-six ...................... 97 ... quatre-vingt-dix-sept
87 ... quatre-vingt-sept ..................... 98 ... quatre-vingt-dix-huit
88 ... quatre-vingt-huit ..................... 99 ... quatre-vingt-dix-neuf
89 ... quatre-vingt-neuf ..................... 100 ... cent
90 ... quatre-vingt-dix ...................... 101 ... cent-un
So, if we start with 5 or CINQ (=4) then ->
English, such as FIVE for the usual 5.
Count the number of characters in the spelling.
In this case, it is 4 — or FOUR.
So, work now with the 4 or FOUR.
Repeat with 4 to get 4 again.
Take, ONE HUNDRED SIXTY-THREE for a total count of 23.
(Include spaces and hyphens in your count.)
ONE HUNDRED SIXTY-THREE -> TWENTY THREE -> TWELVE -> SIX -> THREE -> FIVE -> FOUR.
Try with any other number, and see if it always works
In English we end up with 4 as the final number. It would be interesting to find out what numbers we end up in other languages.
Since I'm fluent in Italian and in French, I'll find out.
Try it in Italian:
Italian Cardinal Numbers: 1 - 100
1 ............... uno ............... (=3)
2 ............... due ............. (=3)
3 ............... tre ............. (=3)
4 ............... quattro ......... (=7)
5 ............... cinque .......... (=6)
6 ............... sei ............. (=3)
7 ............... sette ........... (=5)
8 ............... otto ............ (=4)
9 ............... nove ............ (=4)
10 ............... dieci .......... (=5)
11 ............... undici ......... (=6)
12 ............... dodici ......... (=6)
13 ............... tredici ........ (=7)
14 ............... quattordici ..... (=11)
15 ............... quindici ........ (=8)
16 ............... sedici .......... (=6)
17 ............... diciassette
18 ............... diciotto
19 ............... diciannove
20 ............... venti
21 ............... ventuno
22 ............... ventidue
23 ............... ventitré
24 ............... ventiquattro
25 ............... venticinque
26 ............... ventisei
27 ............... ventisette
28 ............... ventotto
29 ............... ventinove
30 ............... trenta
40 ............... quaranta
50 ............... cinquanta
60 ............... sessanta
70 ............... settanta
80 ............... ottanta
90 ............... novanta
100 ............... cento
So, if we start with 5 or CINQUE (=6) ->
Numbers 1 - 100 in French
1 ... un ............................. 11 ... onze
2 ... deux ........................... 12 ... douze
3 ... trois .......................... 13 ... treize
4 ... quatre ......................... 14 ... quatorze
5 ... cinq ........................... 15 ... quinze
6 ... six ............................ 16 ... seize
7 ... sept ........................... 17 ... dix-sept
8 ... huit ........................... 18 ... dix-huit
9 ... neuf ........................... 19 ... dix-neuf
10 ... dix ........................... 20 ... vingt
21 ... vingt et un ........................ 31 ... trente et un
22 ... vingt-deux ......................... 32 ... trente-deux
23 ... vingt-trois ........................ 33 ... trente-trois
24 ... vingt-quatre ....................... 34 ... trente-quatre
25 ... vingt-cinq ......................... 35 ... trente-cinq
26 ... vingt-six .......................... 36 ... trente-six
27 ... vingt-sept ......................... 37 ... trente-sept
28 ... vingt-huit ......................... 38 ... trente-huit
29 ... vingt-neuf ......................... 39 ... trente-neuf
30 ... trente ............................. 40 ... quarante
41 ... quarante et un ........................... 51 ... cinquante et un
42 ... quarante-deux ............................ 52 ... cinquante-deux
43 ... quarante-trois ........................... 53 ... cinquante-trois
44 ... quarante-quatre .......................... 54 ... cinquante-quatre
45 ... quarante-cinq ............................ 55 ... cinquante-cinq
46 ... quarante-six ............................. 56 ... cinquante-six
47 ... quarante-sept ............................ 57 ... cinquante-sept
48 ... quarante-huit ............................ 58 ... cinquante-huit
49 ... quarante-neuf ............................ 59 ... cinquante-neuf
50 ... cinquante ................................ 60 ... soixante
61 ... soixante et un ........................... 71 ... soixante et onze
62 ... soixante-deux ............................ 72 ... soixante-douze
63 ... soixante-trois ........................... 73 ... soixante-treize
64 ... soixante-quatre .......................... 74 ... soixante-quatorze
65 ... soixante-cinq ............................ 75 ... soixante-quinze
66 ... soixante-six ............................. 76 ... soixante-seize
67 ... soixante-sept ............................ 77 ... soixante-dix-sept
68 ... soixante-huit ............................ 78 ... soixante-dix-huit
69 ... soixante-neuf ............................ 79 ... soixante-dix-neuf
70 ... soixante-dix ............................. 80 ... quatre-vingts
80 ... quatre-vingts ......................... 91 ... quatre-vingt-onze
81 ... quatre-vingt-un ....................... 92 ... quatre-vingt-douze
82 ... quatre-vingt-deux ..................... 93 ... quatre-vingt-treize
83 ... quatre-vingt-trois .................... 94 ... quatre-vingt-quatorze
84 ... quatre-vingt-quatre ................... 95 ... quatre-vingt-quinze
85 ... quatre-vingt-cinq ..................... 96 ... quatre-vingt-seize
86 ... quatre-vingt-six ...................... 97 ... quatre-vingt-dix-sept
87 ... quatre-vingt-sept ..................... 98 ... quatre-vingt-dix-huit
88 ... quatre-vingt-huit ..................... 99 ... quatre-vingt-dix-neuf
89 ... quatre-vingt-neuf ..................... 100 ... cent
90 ... quatre-vingt-dix ...................... 101 ... cent-un
So, if we start with 5 or CINQ (=4) then ->
Palindromic time
A 24-hour digital watch has many times that are palindromic.
For example, 1:01:01, 2:41:42, 23:55:32, 3:59:53, 13:22:31, etc.
For example, 1:01:01, 2:41:42, 23:55:32, 3:59:53, 13:22:31, etc.
(Ignore the colons)
These curious combinations occur 660 times a day.
(1) Find the closest such times.
(2) Find the two palindromes whose difference is closest to 12 hours.
(3) Find the longest time span without a palindromic time.
(1) Find the closest such times.
(2) Find the two palindromes whose difference is closest to 12 hours.
(3) Find the longest time span without a palindromic time.
Monday, February 21, 2011
Having 10 numbers...
Having 10 numbers less than 100, is it always possible to select two disjoint subsets having the same sum?
a 9-digit number such that
Make a 9-digit number of the digits 1, ... ,9 such that
the number created by the first n digits is divisible by n.
Prove that the solution is unique.
the number created by the first n digits is divisible by n.
Prove that the solution is unique.
sum of digits is divisible by 13
Prove that between every 79 successive natural numbers there exists at least
one whose sum of digits is divisible by 13.
Find a sequence of 78 successive natural numbers with the property that
the sum of digits of any of its members is not divisible by 13.
the sum of digits of any of its members is not divisible by 13.
Collatz Problem
"Mathematics is not yet ready for such problems."
The Sum of Its Parts
This is a famous problem.
One says that 10 is divided into three parts and if the small part is multiplied by itself and added to the middle one multiplied by itself the result is the large one multiplied by itself, and when the small part is multiplied by the large part, it equals the middle part multiplied by itself. Find the parts.
Statement #1: 10 is divided into three parts
Statement #2: if the small part is multiplied by itself and added to the middle one multiplied by itself the result is the large one multiplied by itself
Giving ..................................... x^2 + y^2 = z^2
Statement #3: when the small part is multiplied by the large part, it equals the middle part multiplied by itself
Giving ..................................... x * y = z^2
Hint: The answer is: x = 2.57066; y = 3.26993; z = 4.15941
Show how you can find these results.
One says that 10 is divided into three parts and if the small part is multiplied by itself and added to the middle one multiplied by itself the result is the large one multiplied by itself, and when the small part is multiplied by the large part, it equals the middle part multiplied by itself. Find the parts.
http://mathdl.maa.org/mathDL/46/?pa=content&sa=viewDocument&nodeId=2376
Abu Kamil, Algebra (ca 900)
Abu Kamil, Algebra (ca 900)
Statement #1: 10 is divided into three parts
Giving .................................... x + y + z = 10
Statement #2: if the small part is multiplied by itself and added to the middle one multiplied by itself the result is the large one multiplied by itself
Giving ..................................... x^2 + y^2 = z^2
Statement #3: when the small part is multiplied by the large part, it equals the middle part multiplied by itself
Giving ..................................... x * y = z^2
Hint: The answer is: x = 2.57066; y = 3.26993; z = 4.15941
Show how you can find these results.
Goldbach's comet
Origami
Robert Lang folds way-new origami
Robert Lang is a pioneer of the newest kind of origami -- using math and engineering principles to fold mind-blowingly intricate designs that are beautiful and, sometimes, very useful.
Robert Lang merges mathematics with aesthetics to fold elegant modern origami. His scientific approach helps him make folds once thought impossible -- and has secured his place as one of the first… Full bio and more links
Transcript :
My talk is "Flapping Birds and Space Telescopes." And you would think that should have nothing to do with one another, but I hope by the end of these 18 minutes, you'll see a little bit of a relation. It ties to origami. So let me start. What is origami? Most people think they know what origami is. It's this: flapping birds, toys, cootie catchers, that sort of thing. And that is what origami used to be. But it's become something else. It's become an art form, a form of sculpture.
The common theme -- what makes it origami -- is folding, is how we create the form. You know, it's very old. This is a plate from 1797. It shows these women playing with these toys. If you look close, it's this shape, called a crane. Every Japanese kid learns how to fold that crane. So this art has been around for hundreds of years, and you would think something that's been around that long -- so restrictive, folding only -- everything that could done has been done a long time ago. And that might have been the case.
But in the 20th century, a Japanese folder named Yoshizawa came along, and he created tens of thousands of new designs. But even more importantly, he created a language -- a way we could communicate, a code of dots, dashes and arrows. Harkening back to Susan Blackmore's talk, we now have a means of transmitting information with heredity and selection, and we know where that leads. And where it has led in origami is to things like this. This is an origami figure: one sheet, no cuts, folding only, hundreds of folds. This too is origami, and this shows where we've gone in the modern world. Naturalism. Detail. You can get horns, antlers -- even if you look close, cloven hooves.
And it raises a question: what changed? And what changed is something you might not have expected in an art, which is math. That is, people applied mathematical principles to the art, to discover the underlying laws. And that leads to a very powerful tool. The secret to productivity in so many fields -- and in origami -- is letting dead people do your work for you.
(Laughter)
Because what you can do is take your problem and turn it into a problem that someone else has solved, and use their solutions. And I want to tell you how we did that in origami. Origami revolves around crease patterns. The crease pattern shown here is the underlying blueprint for an origami figure. And you can't just draw them arbitrarily. They have to obey four simple laws. And they're very simple, easy to understand. The first law is two-colorability. You can color any crease pattern with just two colors without ever having the same color meeting. The directions of the folds at any vertex -- the number of mountain folds, the number of valley folds -- always differs by two. Two more or two less. Nothing else. If you look at the angles around the fold, you find that if you number the angles in a circle, all the even-numbered angles add up to a straight line. All the odd-numbered angles add up to a straight line. And if you look at how the layers stack, you'll find that no matter how you stack folds and sheets, a sheet can never penetrate a fold. So that's four simple laws. That's all you need in origami. All of origami comes from that.
And you'd think, "Can four simple laws give rise to that kind of complexity?" But indeed, the laws of quantum mechanics can be written down on a napkin, and yet they govern all of chemistry, all of life, all of history. If we obey these laws, we can do amazing things. So in origami, to obey these laws, we can take simple patterns -- like this repeating pattern of folds, called textures -- and by itself it's nothing. But if we follow the laws of origami, we can put these patterns into another fold that itself might be something very, very simple, but when we put it together, we get something a little different. This fish, 400 scales -- again, it is one uncut square, only folding. And if you don't want to fold 400 scales, you can back off and just do a few things, and add plates to the back of a turtle, or toes. Or you can ramp up and go up to 50 stars on a flag, with 13 stripes. And if you want to go really crazy, 1,000 scales on a rattlesnake. And this guy's on display downstairs, so take a look if you get a chance.
The most powerful tools in origami have related to how we get parts of creatures. And I can put it in this simple equation. We take an idea, combine it with a square, and you get an origami figure.
(Laughter)
What matters is what we mean by those symbols. And you might say, "Can you really be that specific? I mean, a stag beetle -- it's got two points for jaws, it's got antennae. Can you be that specific in the detail?" And yeah, you really can. So how do we do that? Well, we break it down into a few smaller steps. So let me stretch out that equation. I start with my idea. I abstract it. What's the most abstract form? It's a stick figure. And from that stick figure, I somehow have to get to a folded shape that has a part for every bit of the subject. A flap for every leg. And then once I have that folded shape that we call the base, you can make the legs narrower, you can bend them, you can turn it into the finished shape.
Now the first step: pretty easy. Take an idea, draw a stick figure. The last step is not so hard, but that middle step -- going from the abstract description to the folded shape -- that's hard. But that's the place where the mathematical ideas can get us over the hump. And I'm going to show you all how to do that so you can go out of here and fold something. But we're going to start small. This base has a lot of flaps in it. We're going to learn how to make one flap. How would you make a single flap? Take a square. Fold it in half, fold it in half, fold it again, until it gets long and narrow, and then we'll say at the end of that, that's a flap. I could use that for a leg, an arm, anything like that.
What paper went into that flap? Well, if I unfold it and go back to the crease pattern, you can see that the upper left corner of that shape is the paper that went into the flap. So that's the flap, and all the rest of the paper's left over. I can use it for something else. Well, there's other ways of making a flap. There's other dimensions for flaps. If I make the flaps skinnier, I can use a bit less paper. If I make the flap as skinny as possible, I get to the limit of the minimum amount of paper needed. And you can see there, it needs a quarter-circle of paper to make a flap. There's other ways of making flaps. If I put the flap on the edge, it uses a half circle of paper. And if I make the flap from the middle, it uses a full circle. So no matter how I make a flap, it needs some part of a circular region of paper. So now we're ready to scale up. What if I want to make something that has a lot of flaps? What do I need? I need a lot of circles.
And in the 1990s, origami artists discovered these principles and realized we could make arbitrarily complicated figures just by packing circles. And here's where the dead people start to help us out. Because lots of people have studied the problem of packing circles. I can rely on that vast history of mathematicians and artists looking at disc packings and arrangements. And I can use those patterns now to create origami shapes. So we figured out these rules whereby you pack circles, you decorate the patterns of circles with lines according to more rules. That gives you the folds. Those folds fold into a base. You shape the base. You get a folded shape -- in this case, a cockroach. And it's so simple.
(Laughter)
It's so simple that a computer could do it. And you say, "Well, you know, how simple is that?" But computers, you need to be able to describe things in very basic terms, and with this we could. So I wrote a computer program a bunch of years ago called TreeMaker, and you can download it from my website. It's free. It runs on all the major platforms -- even Windows.
(Laughter)
And you just draw a stick figure, and it calculates the crease pattern. It does the circle packing, calculates the crease pattern, and if you use that stick figure that I just showed, which you can kind of tell -- it's a deer, it's got antlers -- you'll get this crease pattern. And if you take this crease pattern, you fold on the dotted lines, you'll get a base that you can then shape into a deer, with exactly the crease pattern that you wanted. And if you want a different deer, not a white-tailed deer, you change the packing, and you can do an elk. Or you could do a moose. Or really, any other kind of deer. These techniques revolutionized this art. We found we could do insects, spiders, which are close -- things with legs, things with legs and wings, things with legs and antennae. And if folding a single praying mantis from a single uncut square wasn't interesting enough, then you could do two praying mantises from a single uncut square. She's eating him. I call it "Snack Time."
And you can do more than just insects. This -- you can put details: toes and claws. A grizzly bear has claws. This tree frog has toes. Actually, lots of people in origami now put toes into their models. Toes have become an origami meme. Because everyone's doing it. You can make multiple subjects. So these are a couple of instrumentalists. The guitar player from a single square, the bass player from a single square. And if you say, "Well, but the guitar, bass -- that's not so hot. Do a little more complicated instrument." Well, then you could do an organ.
(Laughter)
And what this has allowed is the creation of origami-on-demand. So now people can say, I want exactly this and this and this, and you can go out and fold it. And sometimes you create high art, and sometimes you pay the bills by doing some commercial work. But I want to show you some examples. Everything you'll see here, except the car, is origami.
(Video)
(Applause)
Just to show you, this really was folded paper. Computers made things move, but these were all real folded objects that we made. And we can use this not just for visuals, but it turns out to be useful even in the real world. Surprisingly, origami, and the structures that we've developed in origami, turn out to have applications in medicine, in science, in space, in the body, consumer electronics and more.
And I want to show you some of these examples. One of the earliest was this pattern: this folded pattern, studied by Koryo Miura, a Japanese engineer. He studied a folding pattern, and realized this could fold down into an extremely compact package that had a very simple opening and closing structure. And he used it to design this solar array. It's an artist's rendition, but it flew in a Japanese telescope in 1995. Now, there is actually a little origami in the James Webb space telescope, but it's very simple. The telescope -- going up in space, it unfolds in two places. It folds in thirds. It's a very simple pattern -- you wouldn't even call that origami. They certainly didn't need to talk to origami artists.
But if you want to go higher and go larger than this, then you might need some origami. Engineers at Lawrence Livermore National Lab had an idea for a telescope much larger. They called it "The Eyeglass." The design called for geosynchronous orbit, 26,000 miles up, 100-meter diameter lens. So, imagine a lens the size of a football field. There were two groups of people who were interested in this: planetary scientists who want to look up, and then other people who wanted to look down. Whether you look up or look down, how do you get it up in space? You've got to get it up there in a rocket. And rockets are small. So you have to make it smaller. How do you make a large sheet of glass smaller? Well, about the only way is to fold it up somehow. So you have to do something like this -- this was a small model.
For the lens, you divide up the panels, you add flexures. But this pattern's not going to work to get something 100 meters down to a few meters. So the Livermore engineers, wanting to make use of the work of dead people, or perhaps live origamists, said, "Let's see if someone else is doing this sort of thing." So they looked into the origami community, we got in touch with them, and I started working with them. And we developed a pattern together that scales to arbitrarily large size, but that allows any flat ring or disc to fold down into a very neat, compact cylinder. And they adopted that for their first generation, which was not 100 meters -- it was a five-meter. But this is a five-meter telescope -- has about a quarter-mile focal length. And it works perfectly on its test range, and it indeed folds up into a neat little bundle.
Now, there is other origami in space. Japan Aerospace [Exploration] Agency flew a solar sail, and you can see here that the sail expands out, and you can still see the fold lines. The problem that's being solved here is something that needs to be big and sheet-like at its destination, but needs to be small for the journey. And that works whether you're going into space, or whether you're just going into a body. And this example is the latter. This is a heart stent developed by Zhong You at Oxford University. It holds open a blocked artery when it gets to its destination, but it needs to be much smaller for the trip there, through your blood vessels. And this stent folds down using an origami pattern, based on a model called the water-bomb base.
Airbag designers also have the problem of getting flat sheets into a small space. And they want to do their design by simulation. So they need to figure out how, in a computer, to flatten an airbag. And the algorithms that we developed to do insects turned out to be the solution for airbags to do their simulation. And so they can do a simulation like this. Those are the origami creases forming, and now you can see the airbag inflate and find out: does it work? And that leads to a really interesting idea.
You know, where did these things come from? Well, the heart stent came from that little blow-up box that you might have learned in elementary school. It's the same pattern, called "the water-bomb base." The airbag-flattening algorithm came from all the developments of circle packing and the mathematical theory that was really developed just to create insects -- things with legs. The thing is, that this often happens in math and science. When you get math involved, problems that you solve for aesthetic value only, or to create something beautiful, turn around and turn out to have an application in the real world. And as weird and surprising as it may sound, origami may someday even save a life. Thanks.
Robert Lang is a pioneer of the newest kind of origami -- using math and engineering principles to fold mind-blowingly intricate designs that are beautiful and, sometimes, very useful.
Robert Lang merges mathematics with aesthetics to fold elegant modern origami. His scientific approach helps him make folds once thought impossible -- and has secured his place as one of the first… Full bio and more links
Transcript :
My talk is "Flapping Birds and Space Telescopes." And you would think that should have nothing to do with one another, but I hope by the end of these 18 minutes, you'll see a little bit of a relation. It ties to origami. So let me start. What is origami? Most people think they know what origami is. It's this: flapping birds, toys, cootie catchers, that sort of thing. And that is what origami used to be. But it's become something else. It's become an art form, a form of sculpture.
The common theme -- what makes it origami -- is folding, is how we create the form. You know, it's very old. This is a plate from 1797. It shows these women playing with these toys. If you look close, it's this shape, called a crane. Every Japanese kid learns how to fold that crane. So this art has been around for hundreds of years, and you would think something that's been around that long -- so restrictive, folding only -- everything that could done has been done a long time ago. And that might have been the case.
But in the 20th century, a Japanese folder named Yoshizawa came along, and he created tens of thousands of new designs. But even more importantly, he created a language -- a way we could communicate, a code of dots, dashes and arrows. Harkening back to Susan Blackmore's talk, we now have a means of transmitting information with heredity and selection, and we know where that leads. And where it has led in origami is to things like this. This is an origami figure: one sheet, no cuts, folding only, hundreds of folds. This too is origami, and this shows where we've gone in the modern world. Naturalism. Detail. You can get horns, antlers -- even if you look close, cloven hooves.
And it raises a question: what changed? And what changed is something you might not have expected in an art, which is math. That is, people applied mathematical principles to the art, to discover the underlying laws. And that leads to a very powerful tool. The secret to productivity in so many fields -- and in origami -- is letting dead people do your work for you.
(Laughter)
Because what you can do is take your problem and turn it into a problem that someone else has solved, and use their solutions. And I want to tell you how we did that in origami. Origami revolves around crease patterns. The crease pattern shown here is the underlying blueprint for an origami figure. And you can't just draw them arbitrarily. They have to obey four simple laws. And they're very simple, easy to understand. The first law is two-colorability. You can color any crease pattern with just two colors without ever having the same color meeting. The directions of the folds at any vertex -- the number of mountain folds, the number of valley folds -- always differs by two. Two more or two less. Nothing else. If you look at the angles around the fold, you find that if you number the angles in a circle, all the even-numbered angles add up to a straight line. All the odd-numbered angles add up to a straight line. And if you look at how the layers stack, you'll find that no matter how you stack folds and sheets, a sheet can never penetrate a fold. So that's four simple laws. That's all you need in origami. All of origami comes from that.
And you'd think, "Can four simple laws give rise to that kind of complexity?" But indeed, the laws of quantum mechanics can be written down on a napkin, and yet they govern all of chemistry, all of life, all of history. If we obey these laws, we can do amazing things. So in origami, to obey these laws, we can take simple patterns -- like this repeating pattern of folds, called textures -- and by itself it's nothing. But if we follow the laws of origami, we can put these patterns into another fold that itself might be something very, very simple, but when we put it together, we get something a little different. This fish, 400 scales -- again, it is one uncut square, only folding. And if you don't want to fold 400 scales, you can back off and just do a few things, and add plates to the back of a turtle, or toes. Or you can ramp up and go up to 50 stars on a flag, with 13 stripes. And if you want to go really crazy, 1,000 scales on a rattlesnake. And this guy's on display downstairs, so take a look if you get a chance.
The most powerful tools in origami have related to how we get parts of creatures. And I can put it in this simple equation. We take an idea, combine it with a square, and you get an origami figure.
(Laughter)
What matters is what we mean by those symbols. And you might say, "Can you really be that specific? I mean, a stag beetle -- it's got two points for jaws, it's got antennae. Can you be that specific in the detail?" And yeah, you really can. So how do we do that? Well, we break it down into a few smaller steps. So let me stretch out that equation. I start with my idea. I abstract it. What's the most abstract form? It's a stick figure. And from that stick figure, I somehow have to get to a folded shape that has a part for every bit of the subject. A flap for every leg. And then once I have that folded shape that we call the base, you can make the legs narrower, you can bend them, you can turn it into the finished shape.
Now the first step: pretty easy. Take an idea, draw a stick figure. The last step is not so hard, but that middle step -- going from the abstract description to the folded shape -- that's hard. But that's the place where the mathematical ideas can get us over the hump. And I'm going to show you all how to do that so you can go out of here and fold something. But we're going to start small. This base has a lot of flaps in it. We're going to learn how to make one flap. How would you make a single flap? Take a square. Fold it in half, fold it in half, fold it again, until it gets long and narrow, and then we'll say at the end of that, that's a flap. I could use that for a leg, an arm, anything like that.
What paper went into that flap? Well, if I unfold it and go back to the crease pattern, you can see that the upper left corner of that shape is the paper that went into the flap. So that's the flap, and all the rest of the paper's left over. I can use it for something else. Well, there's other ways of making a flap. There's other dimensions for flaps. If I make the flaps skinnier, I can use a bit less paper. If I make the flap as skinny as possible, I get to the limit of the minimum amount of paper needed. And you can see there, it needs a quarter-circle of paper to make a flap. There's other ways of making flaps. If I put the flap on the edge, it uses a half circle of paper. And if I make the flap from the middle, it uses a full circle. So no matter how I make a flap, it needs some part of a circular region of paper. So now we're ready to scale up. What if I want to make something that has a lot of flaps? What do I need? I need a lot of circles.
And in the 1990s, origami artists discovered these principles and realized we could make arbitrarily complicated figures just by packing circles. And here's where the dead people start to help us out. Because lots of people have studied the problem of packing circles. I can rely on that vast history of mathematicians and artists looking at disc packings and arrangements. And I can use those patterns now to create origami shapes. So we figured out these rules whereby you pack circles, you decorate the patterns of circles with lines according to more rules. That gives you the folds. Those folds fold into a base. You shape the base. You get a folded shape -- in this case, a cockroach. And it's so simple.
(Laughter)
It's so simple that a computer could do it. And you say, "Well, you know, how simple is that?" But computers, you need to be able to describe things in very basic terms, and with this we could. So I wrote a computer program a bunch of years ago called TreeMaker, and you can download it from my website. It's free. It runs on all the major platforms -- even Windows.
(Laughter)
And you just draw a stick figure, and it calculates the crease pattern. It does the circle packing, calculates the crease pattern, and if you use that stick figure that I just showed, which you can kind of tell -- it's a deer, it's got antlers -- you'll get this crease pattern. And if you take this crease pattern, you fold on the dotted lines, you'll get a base that you can then shape into a deer, with exactly the crease pattern that you wanted. And if you want a different deer, not a white-tailed deer, you change the packing, and you can do an elk. Or you could do a moose. Or really, any other kind of deer. These techniques revolutionized this art. We found we could do insects, spiders, which are close -- things with legs, things with legs and wings, things with legs and antennae. And if folding a single praying mantis from a single uncut square wasn't interesting enough, then you could do two praying mantises from a single uncut square. She's eating him. I call it "Snack Time."
And you can do more than just insects. This -- you can put details: toes and claws. A grizzly bear has claws. This tree frog has toes. Actually, lots of people in origami now put toes into their models. Toes have become an origami meme. Because everyone's doing it. You can make multiple subjects. So these are a couple of instrumentalists. The guitar player from a single square, the bass player from a single square. And if you say, "Well, but the guitar, bass -- that's not so hot. Do a little more complicated instrument." Well, then you could do an organ.
(Laughter)
And what this has allowed is the creation of origami-on-demand. So now people can say, I want exactly this and this and this, and you can go out and fold it. And sometimes you create high art, and sometimes you pay the bills by doing some commercial work. But I want to show you some examples. Everything you'll see here, except the car, is origami.
(Video)
(Applause)
Just to show you, this really was folded paper. Computers made things move, but these were all real folded objects that we made. And we can use this not just for visuals, but it turns out to be useful even in the real world. Surprisingly, origami, and the structures that we've developed in origami, turn out to have applications in medicine, in science, in space, in the body, consumer electronics and more.
And I want to show you some of these examples. One of the earliest was this pattern: this folded pattern, studied by Koryo Miura, a Japanese engineer. He studied a folding pattern, and realized this could fold down into an extremely compact package that had a very simple opening and closing structure. And he used it to design this solar array. It's an artist's rendition, but it flew in a Japanese telescope in 1995. Now, there is actually a little origami in the James Webb space telescope, but it's very simple. The telescope -- going up in space, it unfolds in two places. It folds in thirds. It's a very simple pattern -- you wouldn't even call that origami. They certainly didn't need to talk to origami artists.
But if you want to go higher and go larger than this, then you might need some origami. Engineers at Lawrence Livermore National Lab had an idea for a telescope much larger. They called it "The Eyeglass." The design called for geosynchronous orbit, 26,000 miles up, 100-meter diameter lens. So, imagine a lens the size of a football field. There were two groups of people who were interested in this: planetary scientists who want to look up, and then other people who wanted to look down. Whether you look up or look down, how do you get it up in space? You've got to get it up there in a rocket. And rockets are small. So you have to make it smaller. How do you make a large sheet of glass smaller? Well, about the only way is to fold it up somehow. So you have to do something like this -- this was a small model.
For the lens, you divide up the panels, you add flexures. But this pattern's not going to work to get something 100 meters down to a few meters. So the Livermore engineers, wanting to make use of the work of dead people, or perhaps live origamists, said, "Let's see if someone else is doing this sort of thing." So they looked into the origami community, we got in touch with them, and I started working with them. And we developed a pattern together that scales to arbitrarily large size, but that allows any flat ring or disc to fold down into a very neat, compact cylinder. And they adopted that for their first generation, which was not 100 meters -- it was a five-meter. But this is a five-meter telescope -- has about a quarter-mile focal length. And it works perfectly on its test range, and it indeed folds up into a neat little bundle.
Now, there is other origami in space. Japan Aerospace [Exploration] Agency flew a solar sail, and you can see here that the sail expands out, and you can still see the fold lines. The problem that's being solved here is something that needs to be big and sheet-like at its destination, but needs to be small for the journey. And that works whether you're going into space, or whether you're just going into a body. And this example is the latter. This is a heart stent developed by Zhong You at Oxford University. It holds open a blocked artery when it gets to its destination, but it needs to be much smaller for the trip there, through your blood vessels. And this stent folds down using an origami pattern, based on a model called the water-bomb base.
Airbag designers also have the problem of getting flat sheets into a small space. And they want to do their design by simulation. So they need to figure out how, in a computer, to flatten an airbag. And the algorithms that we developed to do insects turned out to be the solution for airbags to do their simulation. And so they can do a simulation like this. Those are the origami creases forming, and now you can see the airbag inflate and find out: does it work? And that leads to a really interesting idea.
You know, where did these things come from? Well, the heart stent came from that little blow-up box that you might have learned in elementary school. It's the same pattern, called "the water-bomb base." The airbag-flattening algorithm came from all the developments of circle packing and the mathematical theory that was really developed just to create insects -- things with legs. The thing is, that this often happens in math and science. When you get math involved, problems that you solve for aesthetic value only, or to create something beautiful, turn around and turn out to have an application in the real world. And as weird and surprising as it may sound, origami may someday even save a life. Thanks.
Fun Puzzle: A rider on a horse statue
Sunday, February 20, 2011
The Gamow-Stern Elevator Puzzle
"Obvious" is the most dangerous word in mathematics.
But when waiting for a descending elevator on the sixth floor, precisely the opposite effect was observed; the first elevator to pass was almost always "going up"!
To both Gamow and Stern it seemed almost as if there was a conspiracy to make them wait. In a world in which a conspiracy theory is put forth almost every day, in just about any imaginable setting, this is probably what many people would actually believe.
There is, however, a perfectly logical mathematical explanation for what Gamow and Stern observed.
The case of a building with just one elevator is easy to understand. We imagine that the elevator is continually running, going up and down all day long [2], and so it seems reasonable to assume that, if Gamow requested its service at some arbitrary time, then with probability 1/6 it would be below his floor and with probability 5/6 it would be above his floor.
Therefore, with probability 5/6 it would eventually arrive at his floor going down.
For Stern, it would be just the opposite, i.e., the elevator would, with probability 5/6, be going up when it arrived at his floor. This is what Gamow and Stern wrote and, so far so good, But then they blundered.
As Knuth wrote,
When there is more than one elevator, Gamow and Stern say that the "situation will, of course, remain the same." But this is not true! Many a mathematician has fallen into a similar trap, being misled by something which seems self-evident, and nearly every example of faulty reasoning that has been published is accompanied by the phrase "of course" or its equivalent.
Knuth then quickly demonstrates that if there are two independent elevators,
then the first elevator to arrive at Gamow's floor will be going down with probability 13/18, which is not equal to 5/6 = 15/18.
Knuth's calculation with a Monte Carlo simulation.
Knuth then quickly demonstrates that if there are two independent elevators,
then the first elevator to arrive at Gamow's floor will be going down with probability 13/18, which is not equal to 5/6 = 15/18.
Knuth's calculation with a Monte Carlo simulation.
Also, what is the probability that the first-arriving elevator at Gamow's floor is going down in a three-elevator building?
NOTE:
[2]. As Knuth wrote, "Let us assume that we have an "ideal" elevator system, which everyone knows does not exist, but which makes it possible to give a reasonable analysis. We will assume that each elevator goes continually up and down from the bottom floor to the top floor of the building, and back again in a cyclic fashion (independent of the other elevators). At the moment we begin to wait for an elevator on some given floor of the building [floor 2 for Gamow], we may assume that each elevator in the system is at random point in its cycle, and that each will proceeed at the same rate of speed until one [first] reaches our floor."
http://books.google.com/books?id=bmhuaGP3FOEC&pg=PA45&lpg=PA45&dq=puzzle+math,+george+gamow&source=bl&ots=blGGS32cbB&sig=pxALIB7SbsmEaFM1e41_kJHwUJE&hl=en&ei=BadhTeGFJoTbgQfCzfjmAg&sa=X&oi=book_result&ct=result&resnum=9&ved=0CEYQ6AEwCDgK#v=onepage&q=puzzle%20math%2C%20george%20gamow&f=false
People who ride elevators are often puzzled by a strange probability.
The elevator paradox first appeared in the book Puzzle-Math by the physicist George Gamow and his friend Marvin Stern. In explaining the paradox with one elevator, Gamow and Stern made a small mistake. They stated that the probabilities "of course remain the same" if there are two or more elevators.
Donald Knuth was the first to realize that this is not true. Writing on "The Gamow-Stern Elevator Problem" in the Journal of Recreational Mathematics (July 1969), Knuth showed that as the number of elevator increases, the probability that the first elevator to stop on any floor is going up approaches 1/2, and the probability it is going down also approaches 1/2.
This situation, in a way, is even more paradoxical than before.
It means that if you wait on a floor near the top and fix your attention
on any given elevator door, the probability is always high that the next time
elevator arrives it will be going up. But the chance that the next elevator
to stop on the floor will be going up, regardless of the shaft it is in,
is a different matter. This probability approaches 1/2 as the number of elevators
approaches infinity. The same is true of down elevators stopping on a floor near the bottom.
We assume, of course, that elevators travel independently of one another,
with constant speeds, and have the same average waiting time on each floor.
If there are just a few elevators, the changes in probability are slight,
but if there are 20 or more, the probability gets very close to 1/2 for all floors
except the top and bottom ones.
NOTE:
[2]. As Knuth wrote, "Let us assume that we have an "ideal" elevator system, which everyone knows does not exist, but which makes it possible to give a reasonable analysis. We will assume that each elevator goes continually up and down from the bottom floor to the top floor of the building, and back again in a cyclic fashion (independent of the other elevators). At the moment we begin to wait for an elevator on some given floor of the building [floor 2 for Gamow], we may assume that each elevator in the system is at random point in its cycle, and that each will proceeed at the same rate of speed until one [first] reaches our floor."
http://books.google.com/books?id=bmhuaGP3FOEC&pg=PA45&lpg=PA45&dq=puzzle+math,+george+gamow&source=bl&ots=blGGS32cbB&sig=pxALIB7SbsmEaFM1e41_kJHwUJE&hl=en&ei=BadhTeGFJoTbgQfCzfjmAg&sa=X&oi=book_result&ct=result&resnum=9&ved=0CEYQ6AEwCDgK#v=onepage&q=puzzle%20math%2C%20george%20gamow&f=false
If you have an office on a floor near the top.
The first elevator to stop is going up.
Suppose you work on a floor near the bottom.
It happens a lot.
Suppose you work on a floor near the bottom.
Every day you eat lunch in a restaurant on the top floor.
Whenever you want an elevator, the first one to arrive is usually going down.
Donald Knuth was the first to realize that this is not true. Writing on "The Gamow-Stern Elevator Problem" in the Journal of Recreational Mathematics (July 1969), Knuth showed that as the number of elevator increases, the probability that the first elevator to stop on any floor is going up approaches 1/2, and the probability it is going down also approaches 1/2.
This situation, in a way, is even more paradoxical than before.
It means that if you wait on a floor near the top and fix your attention
on any given elevator door, the probability is always high that the next time
elevator arrives it will be going up. But the chance that the next elevator
to stop on the floor will be going up, regardless of the shaft it is in,
is a different matter. This probability approaches 1/2 as the number of elevators
approaches infinity. The same is true of down elevators stopping on a floor near the bottom.
We assume, of course, that elevators travel independently of one another,
with constant speeds, and have the same average waiting time on each floor.
If there are just a few elevators, the changes in probability are slight,
but if there are 20 or more, the probability gets very close to 1/2 for all floors
except the top and bottom ones.
Source:
Conjectures
(1) 2201 is the only non-palindrome known to have a palindromic cube
(2201^3 = 10662526601)
(2) 3375 (=15*15*15) is the largest known cube which contains all prime digits.
(3) 9 is the only known composite number n such that both
(2201^3 = 10662526601)
(2) 3375 (=15*15*15) is the largest known cube which contains all prime digits.
(3) 9 is the only known composite number n such that both
2^n + n^2 and 2^n - n^2 are prime
because 2^9 + 9^2 = 593 and 2^9 - 9^2 = 431
Note : 9 is also the smallest composite number n such that both 2^n + n and 2^n - n
are prime
because 2^9 + 9 = 521 and 2^9 - 9 = 503
How cool is that!
How cool is that!
Saturday, February 19, 2011
Moving staircase
Henry,’ said the professor’s wife, ‘you’re a mathematician. Tell me how many steps there are in that escalator.’
‘Well, Martha, they certainly are difficult to count while they are moving. But if you will walk up, and count the number of steps you take from bottom to top, I think we can find the answer. I will start with you, but will walk twice as fast. Just watch me and take one step every time I take two.’
When Martha reached the top she reported that she had taken just 21 steps, while Henry had taken 28. The professor was then able to tell her exactly how many steps were in sight at one time on the moving staircase.
How many were there?
‘Well, Martha, they certainly are difficult to count while they are moving. But if you will walk up, and count the number of steps you take from bottom to top, I think we can find the answer. I will start with you, but will walk twice as fast. Just watch me and take one step every time I take two.’
When Martha reached the top she reported that she had taken just 21 steps, while Henry had taken 28. The professor was then able to tell her exactly how many steps were in sight at one time on the moving staircase.
How many were there?
64 identical square rooms
A castle consists of 64 identical square rooms, having a door in every wall and arranged in an 8 x 8 square. All the floors are colored white. Every morning a painter walks through the castle recoloring floors in all the rooms he visits from white to black and vice versa.
Is it possible that some day the rooms will be colored as a standard chessboard is?
Is it possible that some day the rooms will be colored as a standard chessboard is?
3 nonintersecting circles of different sizes
Points in an infinite plane
Each point in an infinite plane is colored either red or blue.
Prove that there are two points of the same color that are exactly 1 meter apart.
Game theory: The Truel
You may have seen the movie "The Good, The Bad and the Ugly". Here's a scene at the end of the movie
Suppose that you must participate in a three-way duel with two rivals. Each of you is given a pistol and unlimited ammunition. Unfortunately, you, Red, are the weakest shot — you hit your target only 1/3 of the time. Black is successful 2/3 of the time, and Gray hits everything he aims at.
It’s agreed that you will take turns: You’ll shoot first, then Black, then Gray, and you’ll continue in this order until one survivor remains. At whom should you shoot?
Suppose that you must participate in a three-way duel with two rivals. Each of you is given a pistol and unlimited ammunition. Unfortunately, you, Red, are the weakest shot — you hit your target only 1/3 of the time. Black is successful 2/3 of the time, and Gray hits everything he aims at.
It’s agreed that you will take turns: You’ll shoot first, then Black, then Gray, and you’ll continue in this order until one survivor remains. At whom should you shoot?
Dice puzzles
In the following puzzle the die has 6 sides, with each side having a different number of spots. The numbers go from 1 through 6.
The total number of events in rolling a dice 'n' times is given by 6^n
In our case, the die is rolled 3 times, so n = 3
so total number of events = 6^3 = 6*6*6 = 216 events
The die is rolled three times and the outcome of each roll is noted.
For example (as shown in the video), the numbers are 6, 3, 4
Then, the next step is to reverse the number 634, giving 436
Then subtract: 634 - 436 = 198
The reverse of 198 is 891
Now add these two numbers: 198 + 891 = 1089
How is this trick done?
The total number of events in rolling a dice 'n' times is given by 6^n
In our case, the die is rolled 3 times, so n = 3
so total number of events = 6^3 = 6*6*6 = 216 events
The die is rolled three times and the outcome of each roll is noted.
For example (as shown in the video), the numbers are 6, 3, 4
Then, the next step is to reverse the number 634, giving 436
Then subtract: 634 - 436 = 198
The reverse of 198 is 891
Now add these two numbers: 198 + 891 = 1089
How is this trick done?
Friday, February 18, 2011
Space filling curves
Curve
An interesting question: Where would you be if you started at the lower right and traveled a third of the way along his recursively defined curve?
Some combinatorial applications of spacefilling curves
Hilbert Space Filling Curve Abstract Geometric Art
For example, it has been used as a basis for the rapid construction of an approximate solution to the Traveling Salesman Problem (which asks for the shortest sequence of a given set of points): The heuristic is simply to visit the points in the same sequence as they appear on the Sierpiński curve
An Elementary Proof that Schoenberg's Space-Filling Curve Is Differentiable
Plane Filling Curves: Hilbert's & Moore's
N.B. Different disciplines within mathematics have given the term different meanings depending on the area of study, so the precise meaning depends on context.
It was an exciting event in the history of mathematics when in 1890, the Italian mathematician Peano constructed a continuous curve which passed through every point in the unit square.
Examples of such `space-filling' curves were later constructed by Hilbert (in 1891),
Moore (in 1900) , Lebesgue (in 1904), Sierpinski (in 1912) and Schoenberg (in 1938) . These have come to be known as Peano curves
Hilbert curve
An interesting question: Where would you be if you started at the lower right and traveled a third of the way along his recursively defined curve?
Multidimensional Space-Filling Curves
Sierpiński curve
Lebesgue 3D Curves
Schoenberg Plane-Filling Curve
Subscribe to:
Comments (Atom)