Wednesday, May 25, 2011
Tuesday, May 24, 2011
MOBIUS FUNCTION
http://www.gaussianmath.com/misc/mobiusfunction/mobius.html
Introduction to the Möbius Function
Hat 0
Fundamental Theorem of Arithmetic
Mertens Function
Mertens Conjecture
Identities and Mobidromes
Hat 0
Fundamental Theorem of Arithmetic
Uniqueness of Factorization
Mertens Function
Mertens Conjecture
Identities and Mobidromes
Mathematical Wormhole 1 & 2
Time travel is possible in mathematics!
Check out ... http://www.gaussianmath.com/
for a more indepth explanation and other interesting topics in mathematics
Check out ... http://www.gaussianmath.com/
for a more indepth explanation and other interesting topics in mathematics
The M&M game
It has been said that, "Life is like a box of chocolates—you never know what you're going to get." (Forrest Gump in Forrest Gump, 1994.) In this experiment you can test the "Forrest Gump Chaos Theory" by using M&M's, which are much cheaper than a box of chocolates. What if life is more like a bag of M&M's?
We start with two bags of M&Ms, one with 19 and one with 20.
We start with two bags of M&Ms, one with 19 and one with 20.
In her turn, a player has to eat all the M&Ms in one of the bags, and then split the M&M from the other bag between the two, leaving at least one on each bag, and not necessarily evenly. The she gives the two bags to the other player. The player who receives two bags with one M&M each loses as he can no longer move.
Mathematical Platonism
http://www.lehman.edu/deanhum/philosophy/platofootnote/PlatoFootnote.org/Outreach_files/Mathematical%20Platonism.pdf
Read:
James Robert Brown’s Philosophy of Mathematics: A Contemporary Introduction to the World of Proofs and Pictures (Routledge, 2008).
There is a difference between general Platonism and the mathematical flavor. For Plato, each apple, say, is but an imperfect example of the absolute (and perfect) Idea of an apple. But as Aristotle quickly realized, Plato has it exactly backwards: we arrive at the general idea of ‘apple’ by mentally abstracting a set of characteristics we think common to all actual apples. It is we who conjure the ‘perfect’ idea from the world, not the world copying the concept.
Read:
James Robert Brown’s Philosophy of Mathematics: A Contemporary Introduction to the World of Proofs and Pictures (Routledge, 2008).
There is a difference between general Platonism and the mathematical flavor. For Plato, each apple, say, is but an imperfect example of the absolute (and perfect) Idea of an apple. But as Aristotle quickly realized, Plato has it exactly backwards: we arrive at the general idea of ‘apple’ by mentally abstracting a set of characteristics we think common to all actual apples. It is we who conjure the ‘perfect’ idea from the world, not the world copying the concept.
But now contrast the idea of an apple with the idea of a circle. Here Aristotle’s approach becomes more problematic, as we don’t find any true circles in nature. No natural object has the precise geometric characteristics of a circle, and in a very strong sense we can also say that the circles we draw are but imperfect representations of the perfect idea of a circle. Ah – but whence does such a perfect idea come from?
Consider another way to put the problem. One major difference between science and technology is that science discovers things, while technology is about human inventions. We discover the law of gravity; but we invent airplanes to allow heavier-than-air flight despite the law of gravity. But where do mathematical objects, like circles and numbers, or mathematical theorems like the Pythagorean one, or Fermat’s Last one, come from? Are they inventions of the human mind, or are they discoveries?
Consider another way to put the problem. One major difference between science and technology is that science discovers things, while technology is about human inventions. We discover the law of gravity; but we invent airplanes to allow heavier-than-air flight despite the law of gravity. But where do mathematical objects, like circles and numbers, or mathematical theorems like the Pythagorean one, or Fermat’s Last one, come from? Are they inventions of the human mind, or are they discoveries?
Monday, May 23, 2011
Which of the following statements are true?
1. Precisely one of these statements is untrue.
2. Precisely two of these statements are untrue.
3. Precisely three of these statements are untrue.
4. Precisely four of these statements are untrue.
5. Precisely five of these statements are untrue.
6. Precisely six of these statements are untrue.
7. Precisely seven of these statements are untrue.
8. Precisely eight of these statements are untrue.
9. Precisely nine of these statements are untrue.
10. Precisely ten of these statements are untrue.
2. Precisely two of these statements are untrue.
3. Precisely three of these statements are untrue.
4. Precisely four of these statements are untrue.
5. Precisely five of these statements are untrue.
6. Precisely six of these statements are untrue.
7. Precisely seven of these statements are untrue.
8. Precisely eight of these statements are untrue.
9. Precisely nine of these statements are untrue.
10. Precisely ten of these statements are untrue.
Sunday, May 22, 2011
Sum of two dice
2 .................. 1+1 .................................................1/36
3 ...................1+2, 2+1 ..........................................2/36
4 ...................1+3, 2+2, 3+1 ..................................3/36
5 ...................1+4, 2+3, 3+2, 4+1 .........................4/36
6 ...................1+5, 2+4, 3+3, 4+2, 5+1 .................5/36
7 ...................1+6, 2+5, 3+4, 4+3, 5+2, 6+1 ..........6/36
8 ...................2+6, 3+5, 4+4, 5+3, 6+2 .................5/36
9 ...................3+6, 4+5, 5+4, 6+3 ........................4/36
10 ..................4+6, 5+5, 6+4 ................................3/36
11 ..................5+6, 6+5 .........................................2/36
12 ..................6+6 ..................................................1/36
Is it possible to load the dice in such a way that these eleven scores are equally probable?
4 ...................1+3, 2+2, 3+1 ..................................3/36
5 ...................1+4, 2+3, 3+2, 4+1 .........................4/36
6 ...................1+5, 2+4, 3+3, 4+2, 5+1 .................5/36
7 ...................1+6, 2+5, 3+4, 4+3, 5+2, 6+1 ..........6/36
8 ...................2+6, 3+5, 4+4, 5+3, 6+2 .................5/36
9 ...................3+6, 4+5, 5+4, 6+3 ........................4/36
10 ..................4+6, 5+5, 6+4 ................................3/36
11 ..................5+6, 6+5 .........................................2/36
12 ..................6+6 ..................................................1/36
Is it possible to load the dice in such a way that these eleven scores are equally probable?
A clock puzzle
Imagine a clock that does not have any hands or numbers on it, but it has a chimer.
If the time is 1 o'clock, it chimes once. If the time is 2 o'clock, it chimes twice, and so forth. The time gap between any two chimes is 3 seconds.
How many seconds would it take you to know the time, after the first chime is heard, if it is 3 o'clock?
Game show: 5 fortune tellers
On a game show there are 5 fortune tellers (A, B, C, D and E)
A has 81% chance of being correct
B ..... 65% .........................................
C ..... 43% .........................................
D...... 35% .........................................
E ...... 8% ............................................
If you were trying to get the best prediction of your future, which fortune teller would you go to?
A has 81% chance of being correct
B ..... 65% .........................................
C ..... 43% .........................................
D...... 35% .........................................
E ...... 8% ............................................
If you were trying to get the best prediction of your future, which fortune teller would you go to?
n times the sum of its digits
Which number is 5 times the sum of its digits?
In general, to find 2-digit and 3-digit numbers that are (2, 3, 4, 5, ...) times the sum of their digits
And any d-digits (d > 3)?
In general, to find 2-digit and 3-digit numbers that are (2, 3, 4, 5, ...) times the sum of their digits
And any d-digits (d > 3)?
Saturday, May 21, 2011
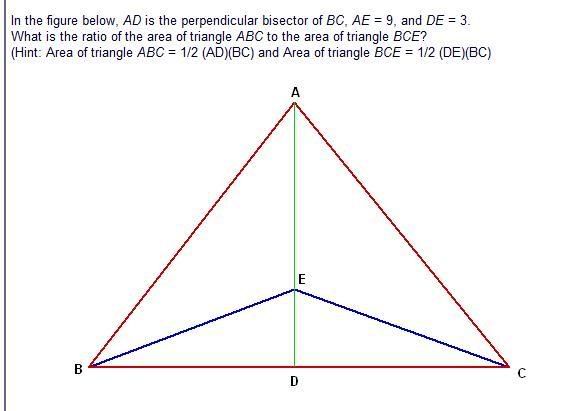
n circles with radius r ...
... are inscribed in a circle with radius 1
Determine the radius r and the area A of the shaded region between the circles for n = 4 and n = 3
Hint: In an equilateral triangle the medians divide each other in the ratio of 2:1
Determine the radius r and the area A of the shaded region between the circles for n = 4 and n = 3
Hint: In an equilateral triangle the medians divide each other in the ratio of 2:1
Sunday, May 15, 2011
Smallest positive integer that includes among its factors perfect squares
1^2 = 1 ..... 2^2 = 4 ..... 3^2 = 9
4^2 = 16 ... 5^2 = 25 ... 6^2 = 36 ... 7^2 = 49 ... 8^2 = 64
The factors of 2304 are:
1 2 3 4 6 8 9 12 16 18 24 32 36 48 64 72 96 128 144 192 256 288 384 576 768 1152 2304
The prime factors are: 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 or 2^8 * 3^2
2304 is the smallest positive integer that includes among its factors at least 10 perfect squares.
4^2 = 16 ... 5^2 = 25 ... 6^2 = 36 ... 7^2 = 49 ... 8^2 = 64
10^2 = 100 ..... 11^2 = 121 ..... 12^2 = 144 ..... 13^2 = 169 ..... 14^2 = 196
15^2 = 225 ..... 16^2 = 256 ..... 17^2 = 289 ..... 18^2 = 324 ..... 19^2 = 361
20^2 = 400 ..... 21^2 = 441 ..... 22^2 = 484 ..... 23^2 = 529 ..... 24^2 = 576
25^2 = 625 ..... 26^2 = 676 ..... 27^2 = 729 ..... 28^2 = 784 ..... 29^2 = 841
30^2 = 900 ..... 31^2 = 961
The factors of 2304 are:
1 2 3 4 6 8 9 12 16 18 24 32 36 48 64 72 96 128 144 192 256 288 384 576 768 1152 2304
The prime factors are: 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2 * 3 * 3 or 2^8 * 3^2
2304 is the smallest positive integer that includes among its factors at least 10 perfect squares.
(sqrt(n)^sqrt(n))^sqrt(n) an integer?
http://www.wolframalpha.com/input/?i=%28sqrt%28n%29^sqrt%28n%29%29^Sqrt%28n%29
For how many integral values of n in the range 1 to 1000 (inclusive) is the following statement true?
Calendar: July : 5 Fridays, 5 Saturdays and 5 Sundays
How often do we have this combination?
July
2005
2011
2016
2022
2033
Other months, for example,
Octobre
2004
The 80-80-20 Triangle
Is there anything else that could be said about the 80-80-20 triangle?
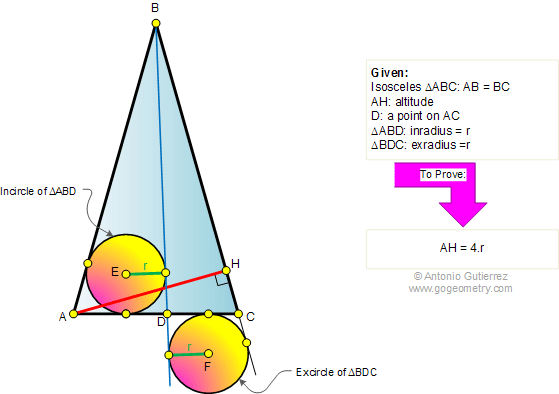
Problem 358. Isosceles triangle 80-80-20, Circle, Angles, Congruence.
Problem 274: Isosceles Triangle, 80-80-20, Angles
Problem 274: Isosceles Triangle, 80-80-20, Angles
Monday, May 9, 2011
A collection of Math Olympiad problems
(1) Find the smallest natural number which is a multiple of 2009 and whose sum of
(decimal) digits equals 2009.
(6) Find all primes p such that p^2 – p + 1 is a perfect cube.
(decimal) digits equals 2009.
(2) Find all integer solutions of the equation 3^x - 5^y = z^2
(3) Solve in integers the equation 12^x + y^4 = 2008^z
(4) Determine all pairs of natural numbers (x, n) that satisfy the equation
(5) Determine all pairs (x, y) of integers such that
x^3 + 2x + 1 = 2^n
(5) Determine all pairs (x, y) of integers such that
1 + 2^x + 2^(2x+1) = y^2
(6) Find all primes p such that p^2 – p + 1 is a perfect cube.
(7) Let a, b, c be positive real numbers. Prove the inequality
(a^2 / b) + (b^2 / c) + (c^2 / a) >= a + b + c + 4(a – b)^2 / (a + b + c)
When does equality occur ? Thursday, May 5, 2011
Wednesday, May 4, 2011
A Proposal to End the Practice of Gerrymandering
Using a precise mathematical formula, it is possible to redraw district lines fairly and bring competitiveness back to congressional races
Drawn Together: Can Math Nerds Beat Gerrymandering?
Gerrymandering: Why Your Vote Doesn't Count
Squares of 2 consecutive even numbers using the same digits
206^2 = 42436 and 208^2 = 43264
Find others
Squares and cubes of 2 numbers using the same digits:
102^2 = 10404 and 201^2 = 40401
102^3 = 1,061,208 and 201^3 = 8,120,601.
Digits
202^3 = 8,242,408 = (–8 + 242 – 40 + 8)^3
204 = 3^2 + 7^2 + 5^2 + 11^2 = 2^2 + 8^2 + 6^2 + 10^2,
where 3+7 = 2+8 and after adding 3 to each digit: 6+10 = 5+11.
204^2 = 23^3 + 24^3 + 25^3 = 41,616.
206^3 = 8,741,816 = (8 + 7 + 4 + 181 + 6)^3
208^3 = 8,998,912 = (08 + 99 + 89 + 12)^3
209 = 1^6 + 2^5 + 3^4 + 4^3 + 5^2 + 6^1
305^3 = 28,372,625 = (283 + 7 + 2 + 6 + 2 + 5)^3
494 + 209 = 703 and 494,209 = 703^2
88+209 = 297 and 88,209 = 297^2 and 494+209 = 703 and 494,209 = 703^2 and 297+703 = 1000
2,401 = (2 + 4 + 0 + 1)^4 = 7^4
10,000 = (1+2+3+4)^4 = [(1^5+2^5+3^5+4^5)+(1^7+2^7+3^7+4^7)]/2
Reversible numbers and their squares:
102^2 = 10404 and 201^2 = 40401.
103^2 = 10609 and 301^2 = 90601.
Square numbers using the same digits:
108^2 = 11664, 129^2 = 16641 and 204^2 = 41616
148^2 = 21904, 203^2 = 41209 and 302^2 = 91204.
102^2 = 10404 ... 120^2 = 14400 ... 201^2 = 40401 ... 210^2 = 44100.
148^2 = 21904 ... 203^2 = 41209 ... 302^2 = 91204.
130^2 = 16900 ... 140^2 = 19600 ... 310^2 = 96100,
103^2 = 10609 ... 247^2 = 61009 ... 301^2 = 90601.
207^2 = 42849, 222^2 = 49284 and 288^2 = 82944
128^2 = 16,384, 178^2 = 31,684, 191^2 = 36,481, 196^2 = 38,416 and 209^2 = 43,681.
Monday, May 2, 2011
tan(4*pi/3) and arctan(4*pi/3)
tan(4*pi/3)
tan(4*pi/3) is clearly an irrational number. How to that arctan(4*pi/3), in radians, is irrational?
Subscribe to:
Posts (Atom)